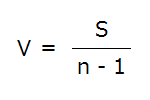相関分析、回帰分析

Top > 情報処理技術者試験の覚書き > QC検定2級 > 相関分析、回帰分析

キーワードは、
　「標本相関係数」
　「無相関性」
　「系列相関」
　「回帰式」
　「最小二乗法」
です。

よく出題されるのは、やはり回帰式でしょうか。これは最低抑えておきたい式です。
回帰に関係して覚えるものは多いです。

そもそも相関分析と回帰分析の違いって何？
特性と要因や要因同士の関係をみるのは相関分析。
ある一定値以上の強度を保証するように制御したするのは回帰分析。
…うーん、難しい。
相関は２つの変数の関係をみるもの、回帰は片方の変数でもう片方を説明することが目的。

標本相関係数

xの偏差平方和


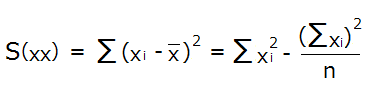
yの偏差平方和


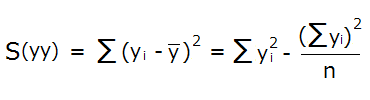
xyの偏差積和


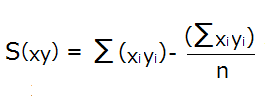
標本相関係数

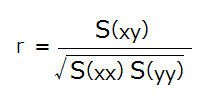
回帰式

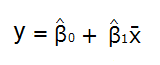
これは絶対覚えないといけません！！
回帰式のβ関連の回帰母数（β0、β1）の求め方は、



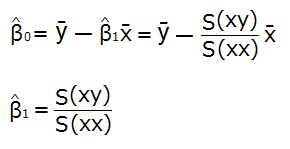
です。

分散分析表

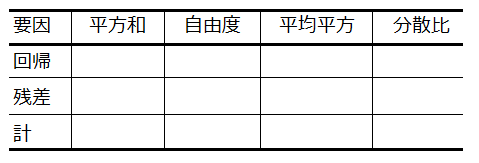
この表が問題に出る確率は80%ぐらいでしょうか！
試験では抜けている項目の値を埋める感じの問いになりますので、全ての枠の値を計算して埋めれるように練習が必要です。

重要なのは、平方和の列、自由度の列と私は思っています。

平方和（回帰）

表の列：平方和、行：回帰の値を求める式です。
上記の「（偏差）平方和（S）」と混同に気をつけないといけません。

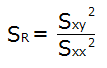
平方和（残差）

表の列：平方和、行：残差の値を求める式です。
表では順番に計算できそうですが、実は↓の「平方和（計）」を先に計算する必要があります。
…なら先に書けよって感じしますが。

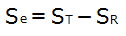
平方和（計）

簡単な計算式です。

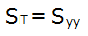
自由度

回帰の自由度：回帰式中の説明変数の数
残差の自由度：全データ数－回帰の自由度－１

平均平方

平方和 ÷ 自由度
例）平方和：１０、自由度：５の場合の平均平方は２

分散費

回帰の平均平方 ÷ 残差の平均平方

分散（V）

平方和の値はデータ数が多くなると大きくなるので、データ数の影響を受けない尺度
分散の計算の仕方も必須ですので、覚えましょう。